3. Trigonometry

d. Trig Identities

2. Parity, Complementarity and Supplementarity Identities

Parity Identities

Sine is an odd function and cosine is an even function: \[ \sin(-\theta)=-\sin(\theta) \qquad \cos(-\theta)=\cos(\theta) \] \(\Leftarrow\Leftarrow\) Read it! It simply explains the plot.

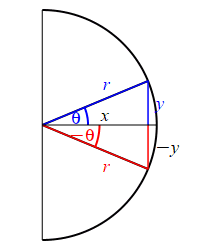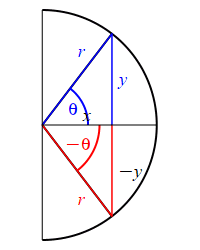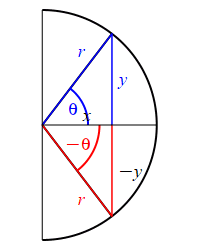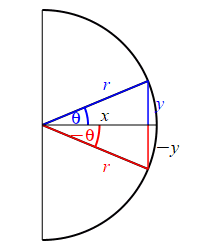
Looking at the figure, the ray at the angle \(\theta\) hits the circle at the point \((x,y)\), while the ray at the angle \(-\theta\) hits the circle at the point \((x,-y)\). So: \[ \sin(\theta)=\dfrac{y}{r} \quad \text{while} \quad \sin(-\theta)=\dfrac{-y}{r}=-\sin(\theta) \] and \[ \cos(\theta)=\dfrac{x}{r} \quad \text{while} \quad \cos(-\theta)=\dfrac{x}{r}=\cos(\theta) \]

The parity of \(\sin\) and \(\cos\) can also be understood by looking at their plots.

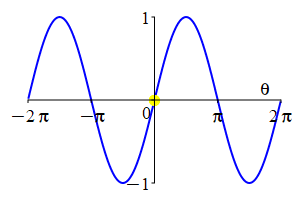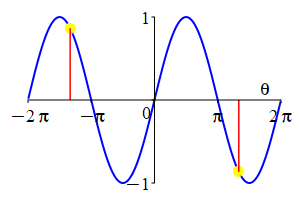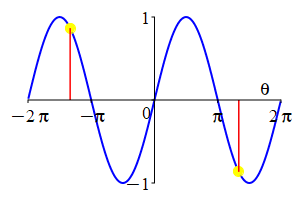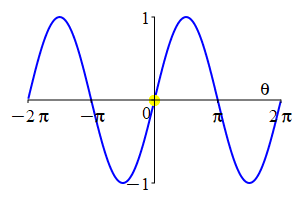
prop_parity_sin_anim — \(\sin(-\theta)=-\sin(\theta)\)

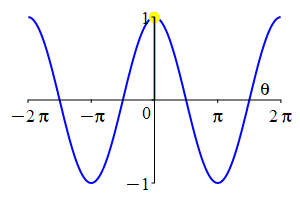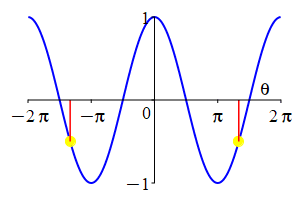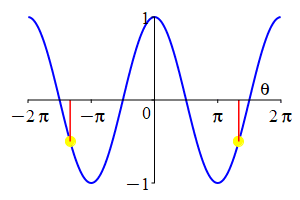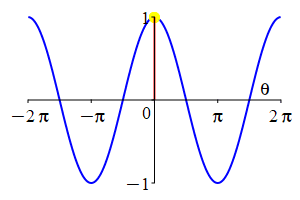
prop_parity_cos_anim — \(\cos(-\theta)=\cos(\theta)\)

As a consequence:

Tangent, cotangent and cosecant are odd functions and secant is an even function: \[ \tan(-\theta)=-\tan(\theta) \qquad \cot(-\theta)=-\cot(\theta) \] \[ \sec(-\theta)=\sec(\theta) \qquad \quad \csc(-\theta)=-\csc(\theta) \] \(\Leftarrow\Leftarrow\) It's a simple computation.

\[ \tan(-\theta)=\dfrac{\sin(-\theta)}{\cos(-\theta)} =\dfrac{-\sin(\theta)}{\cos(\theta)}=-\tan(\theta) \] \[ \cot(-\theta)=\dfrac{\cos(-\theta)}{\sin(-\theta)} =\dfrac{\cos(\theta)}{-\sin(\theta)}=-\cot(\theta) \] \[ \sec(-\theta)=\dfrac{1}{\cos(-\theta)} =\dfrac{1}{\cos(\theta)}=\sec(\theta) \qquad \] \[ \csc(-\theta)=\dfrac{1}{\sin(-\theta)} =\dfrac{1}{-\sin(\theta)}=-\csc(\theta) \]

Complementarity Identities

The complementary angle for \(\theta\) is \(90^\circ-\theta\) or \(\dfrac{\pi}{2}-\theta\). \[ \sin\left(\dfrac{\pi}{2}-\theta\right)=\cos(\theta) \qquad \cos\left(\dfrac{\pi}{2}-\theta\right)=\sin(\theta) \] \(\Leftarrow\Leftarrow\) Read it! It simply explains the plot.

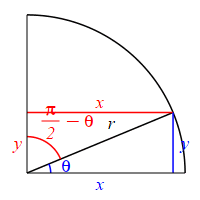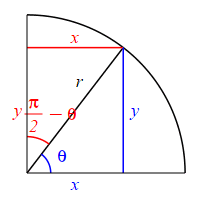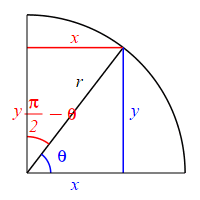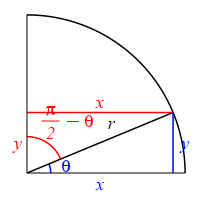
Looking at the figure, if the angle \(\theta\) is measured counterclockwise from the positive \(x\)-axis, then the complementary angle \(\dfrac{\pi}{2}-\theta\) can be measured clockwise from the positive \(y\)-axis. So switching from an angle to its complement is equivalent to a reflection through the \(45^\circ\) diagonal line. This means that the roles of \(x\) and \(y\) are interchanged. (The opposite and adjacent sides are interchanged.) So: \[\begin{aligned} \sin\left(\dfrac{\pi}{2}-\theta\right) &=\dfrac{\text{Opp}}{\text{Hyp}} =\dfrac{x}{r} \\ \cos(\theta) &=\dfrac{\text{Adj}}{\text{Hyp}} =\dfrac{x}{r} \end{aligned}\] and \[\begin{aligned} \cos\left(\dfrac{\pi}{2}-\theta\right) &=\dfrac{\text{Adj}}{\text{Hyp}} =\dfrac{y}{r} \\ \sin(\theta) &=\dfrac{\text{Opp}}{\text{Hyp}} =\dfrac{y}{r} \end{aligned}\]

The complementarity identities can also be understood by comparing the plot of \(\sin(\theta)\) with that of \(\cos\left(\dfrac{\pi}{2}-\theta\right)\) and the plot of \(\cos(\theta)\) with that of \(\sin\left(\dfrac{\pi}{2}-\theta\right)\).

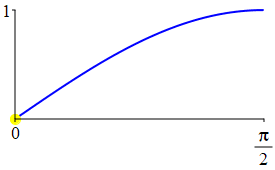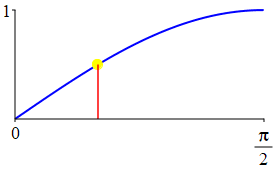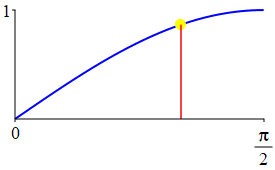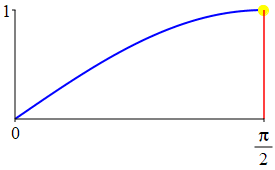
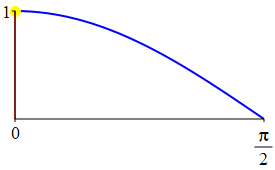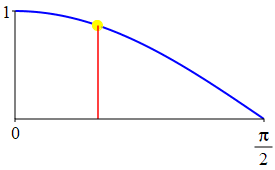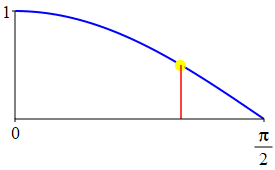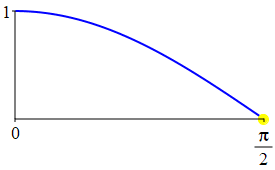
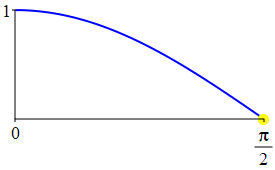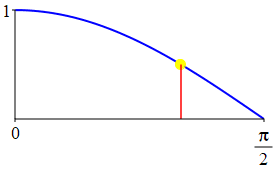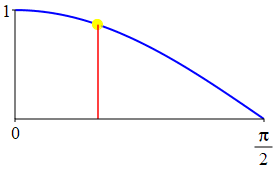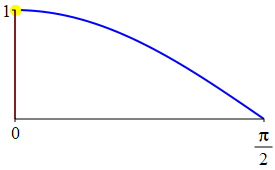
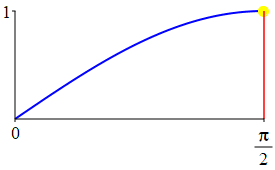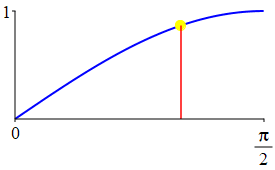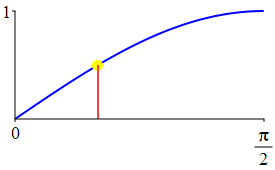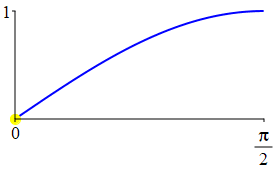
As a consequence:

\[ \tan\left(\dfrac{\pi}{2}-\theta\right)=\cot(\theta) \qquad \cot\left(\dfrac{\pi}{2}-\theta\right)=\tan(\theta) \] \[ \sec\left(\dfrac{\pi}{2}-\theta\right)=\csc(\theta) \qquad \csc\left(\dfrac{\pi}{2}-\theta\right)=\sec(\theta) \] \(\Leftarrow\Leftarrow\) It's a simple computation.

\[ \tan\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{\sin\left(\dfrac{\pi}{2}-\theta\right)}{\cos\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{\cos(\theta)}{\sin(\theta)}=\cot(\theta) \] \[ \cot\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{\cos\left(\dfrac{\pi}{2}-\theta\right)}{\sin\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{\sin(\theta)}{\cos(\theta)}=\tan(\theta) \] \[ \sec\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{1}{\cos\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{1}{\sin(\theta)}=\csc(\theta) \] \[ \csc\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{1}{\sin\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{1}{\cos(\theta)}=\sec(\theta) \]

Notice that switching from an angle to its complementary angle interchanges each trig function with its complementary function: \(\sin\) with \(\cos\), \(\tan\) with \(\cot\), \(\sec\) with \(\csc\). This is, in fact, why they are called “co”-functions.

Supplementarity Identities

The supplementary angle for \(\theta\) is \(180^\circ-\theta\) or \(\pi-\theta\). \[ \sin(\pi-\theta)=\sin(\theta) \qquad \cos(\pi-\theta)=-\cos(\theta) \] \(\Leftarrow\Leftarrow\) Read it! It simply explains the plot.

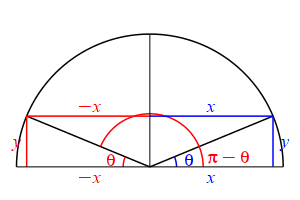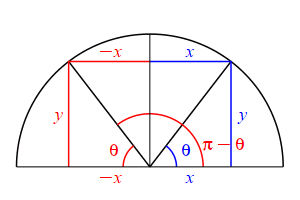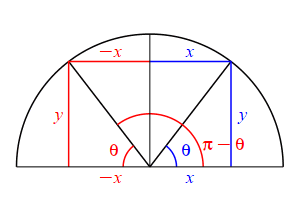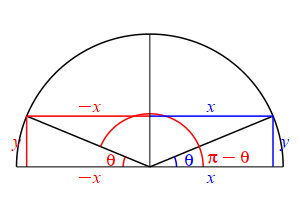
Looking at the figure, the ray at the angle \(\theta\) hits the circle at the point \((x,y)\), while the ray at the angle \(\pi-\theta\) hits the circle at the point \((-x,y)\). So: \[ \sin(\theta)=\dfrac{y}{r} \quad \text{while} \quad \sin(\pi-\theta)=\dfrac{y}{r}=\sin(\theta) \] and \[ \cos(\theta)=\dfrac{x}{r} \quad \text{while} \quad \cos(\pi-\theta)=\dfrac{-x}{r}=-\cos(\theta) \]

The supplementarity identities can also be understood by comparing the plot of \(\sin(\theta)\) with that of \(\sin(\pi-\theta)\) and the plot of \(\cos(\theta)\) with that of \(\cos(\pi-\theta)\).

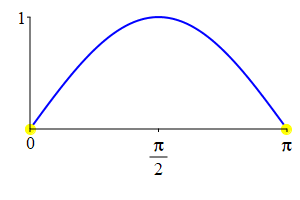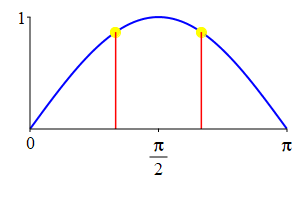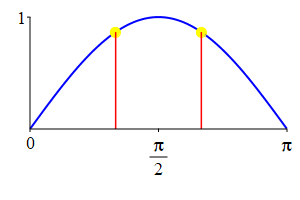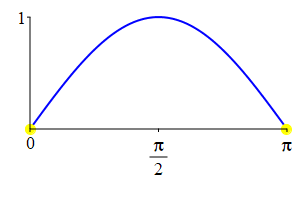
prop_supp_sin_anim — \(\sin(\theta)=\sin(\pi-\theta)\).

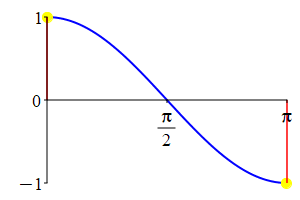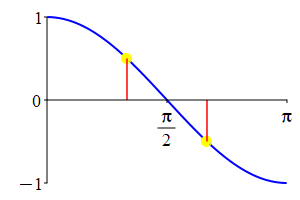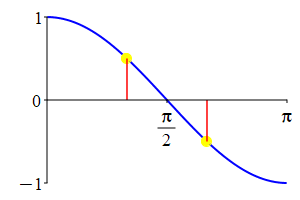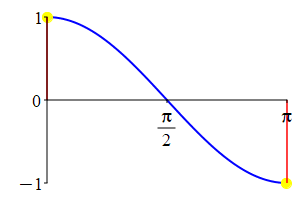
prop_supp_cos_anim — \(\cos(\theta)=-\cos(\pi-\theta)\).

As a consequence:

\[ \tan(\pi-\theta)=-\tan(\theta) \qquad \cot(\pi-\theta)=-\cot(\theta) \] \[ \sec(\pi-\theta)=-\sec(\theta) \qquad \csc(\pi-\theta)=\csc(\theta) \quad \] \(\Leftarrow\Leftarrow\) It's a simple computation.

\[ \tan(\pi-\theta)=\dfrac{\sin(\pi-\theta)}{\cos(\pi-\theta)} =\dfrac{\sin(\theta)}{-\cos(\theta)}=-\tan(\theta) \] \[ \cot(\pi-\theta)=\dfrac{\cos(\pi-\theta)}{\sin(\pi-\theta)} =\dfrac{-\cos(\theta)}{\sin(\theta)}=-\cot(\theta) \] \[ \sec(\pi-\theta)=\dfrac{1}{\cos(\pi-\theta)} =\dfrac{1}{-\cos(\theta)}=-\sec(\theta) \] \[ \csc(\pi-\theta)=\dfrac{1}{\sin(\pi-\theta)} =\dfrac{1}{\sin(\theta)}=\csc(\theta) \qquad \]

Given that \[ \sin60^\circ=\dfrac{\sqrt{3}}{2} \quad \text{and} \quad \cos60^\circ=\dfrac{1}{2} \] find \(\sin(-30^\circ)\) and \(\cos(-30^\circ)\).

We use both the parity and complementarity identities for \(\sin(\theta)\) and \(\cos(\theta)\).
Applying the parity identity and then the complementarity, we see: \[ \sin(-30^\circ) = -\sin(30^\circ)=-\cos(60^\circ)=-\dfrac{1}{2} \] Similarly: \[ \cos(-30^\circ)=\cos(30^\circ)=\sin(60^\circ)=\dfrac{\sqrt{3}}{2} \]

Given that \[ \sin60^\circ=\dfrac{\sqrt{3}}{2} \quad \text{and} \quad \cos60^\circ=\dfrac{1}{2} \] find \(\sin(-150^\circ)\).

Go from \(-150^\circ\) to \(150^\circ\) to \(30^\circ\) to \(60^\circ\).

\(\sin(-150^\circ) = -\dfrac{1}{2}\)

We applying the parity identity for \(\sin\), then the supplementarity identity for \(\sin\) and finally the complementarity identity: \[ \sin(-150^\circ)=-\sin(150^\circ)=-\sin(30^\circ) =-\cos(60^\circ)=-\dfrac{1}{2} \]

3. Trigonometry

d. Trig Identities

2. Parity, Complementarity and Supplementarity Identities

Parity Identities

Complementarity Identities

Supplementarity Identities

Heading